- Libraries and constants
- Dot plot
- Graph of function
- Multi-panel figure
- Density plots
- 2D hexagonal binning plots
- References
- Index of used functions and methods
Matplotlib is a powerful tool for visualizing data and plotting graphs. But that power and flexibility entail many hours of searching the vast documentation for a needed function or a keyword. On this page I gathered the code, with all the neat tricks and the details, for producing publication-ready graphs specifically useful in the domain of natural sciences.
See References for more tutorials and general information about Matplotlib.
Libraries and constants¶
All examples were written in the Jupyter Notebook, but should work in the shell too.
A notebook usually begins with a little magic from IPython, importing key libraries — e.g., Pyplot, pandas, NumPy, sqlite3, and declaring constants — font and color for a consistent look.
%matplotlib inline
%config InlineBackend.figure_format = 'svg'
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import sqlite3
cfont = {'fontname': 'Clear Sans'}
ccolor = '#c3c3c3'
Dot plot¶
Dot plot is an alternative to the more ubiquitous bar chart which uses less ink.
First, collect and sort data with a Series. In this example I use the average one way commuting time from numbeo.com:
ctime_index = pd.Series({
'Amsterdam': 30.07,
'Antwerp': 36.80,
'Barcelona': 30.52,
'Berlin': 33.93,
'Budapest': 38.74,
'Copenhagen': 28.65,
'Dublin': 40.26,
'Hamburg': 32.48,
'Helsinki': 32.23,
'Ljubljana': 28.03,
'Montreal': 39.76,
'Moscow': 52.63,
'Munich': 33.54,
'New York': 43.01,
'Oslo': 32.51,
'Stockholm': 37.56,
'Vienna': 26.55
})
ctime_index.sort_values(inplace=True, ascending=False)
Next, initialize the figure and the axes with subplots function, set transparency off, and hide all four borders. Plot the values of ctime_index rounded by numpy.rint function with circles ('o') as
markers. Draw ticks and tick labels. Adjust limits for both axes, label an x axis, and draw the grid. Save the figure as a PNG file.
fig, ax = plt.subplots(figsize=(4.5, 6)) # (width, height) in inches
fig.patch.set_alpha(1.0) # setting transparency off
ax.spines[:].set_visible(False)
markers = ax.plot(np.rint(ctime_index), range(len(ctime_index)),
'o', markersize=8,
)
ax.tick_params('y', length=10, width=0.5, color=ccolor)
ax.tick_params('x', length=0)
ax.set_yticks(markers[0].get_ydata())
ax.set_yticklabels(ctime_index.index, fontsize='medium')
ax.set_xlim(20, 61.5)
ax.set_ylim(len(ctime_index) - 0.5, -0.4)
ax.set_xlabel(
u'average one way commuting time (minutes)',
fontsize='large', **cfont)
ax.grid(axis='both', linewidth=0.5)
fig.savefig('dot-plot.png', bbox_inches='tight', dpi=300, format='png')
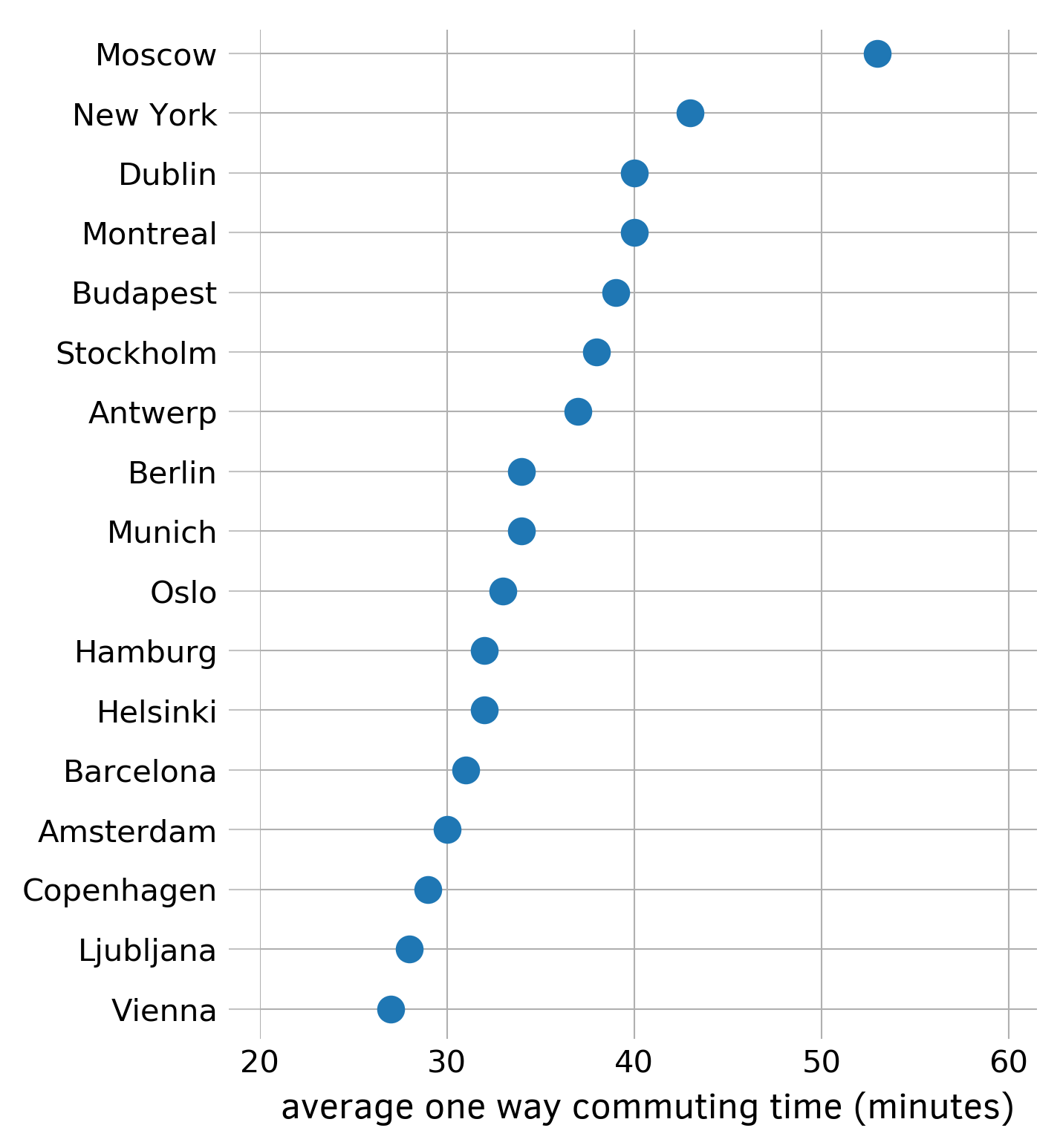
Figure 1: Simple dot plot. Data from numbeo.com
Graph of function¶
In the natural sciences you can’t do without a basic graph of a function with arrowed axes. Here, we draw such graph for the Morse potential.
Define the function and parameters (code by Robert Johansson):
D = 5.0
b = 1.5
args = {'D': D, 'b': b}
x_min = -2*np.pi
x_max = 2*np.pi
N = 750
def U_morse(x, args):
"""
Morse oscillator potential
"""
D = args['D']
b = args['b']
u = D * (1-np.exp(-b*x)) ** 2
return u
Find the minimum point:
from scipy import optimize
x = np.linspace(x_min, x_max, N)
U = U_morse(x, args)
x_opt_min = optimize.fmin(U_morse, [0.0], (args,))
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 3
Function evaluations: 6
Felix Hoffman wrote nice code for drawing axes
with the Axes.arrow method:
fig, ax = plt.subplots(figsize=(6, 4.5)) # (width, height) in inches
fig.patch.set_alpha(1.0) # setting transparency off
ax.spines[:].set_visible(False)
ax.set_xticks(x_opt_min)
ax.set_yticks([])
ax.set_xticklabels([r'$x_e$'], fontsize='x-large', **cfont)
ax.tick_params('both', length=0)
ax.set_xlabel(u'$x$', fontsize='x-large', **cfont)
ax.set_ylabel(u'U($x$)', fontsize='x-large', **cfont)
ax.set_xlim(-2, 5)
ax.set_ylim( 0, 25)
# Drawing arrowed axes using code by Felix Hoffman
# get width and height of axes object to compute
# matching arrowhead length and width
dps = fig.dpi_scale_trans.inverted()
bbox = ax.get_window_extent().transformed(dps)
width, height = bbox.width, bbox.height
xmin, xmax = ax.get_xlim()
ymin, ymax = ax.get_ylim()
# manual arrowhead width and length
hw = 1./20. * (ymax-ymin)
hl = 1./20. * (xmax-xmin)
# compute matching arrowhead length and width
yhw = hw/(ymax-ymin)*(xmax-xmin) * height/width
yhl = hl/(xmax-xmin)*(ymax-ymin) * width/height
# draw x and y axes
ax.arrow(xmin, 0, xmax - xmin, 0,
facecolor='black',
edgecolor='black',
linewidth=1.5,
head_width=hw,
head_length=hl,
overhang=0.5,
length_includes_head=True,
clip_on=False,
)
ax.arrow(-2, ymin, 0, ymax - ymin,
facecolor='black',
edgecolor='black',
linewidth=1.5,
head_width=yhw,
head_length=yhl,
overhang=0.5,
length_includes_head=True,
clip_on=False,
)
ax.hlines(D, xmin, xmax, linestyles='dashed', linewidth=1.5)
ax.annotate(u'',
xy=(x_max/2., D),
xytext=(x_max/2., 0),
arrowprops=dict(arrowstyle='<->', linewidth=1.5),
)
ax.text(x_max/2. + 0.1, D/2.5, u'$D_e$', fontsize='x-large', **cfont)
ax.plot(x, U, linewidth=3)
fig.savefig('morse.png', bbox_inches='tight', dpi=300, format='png')
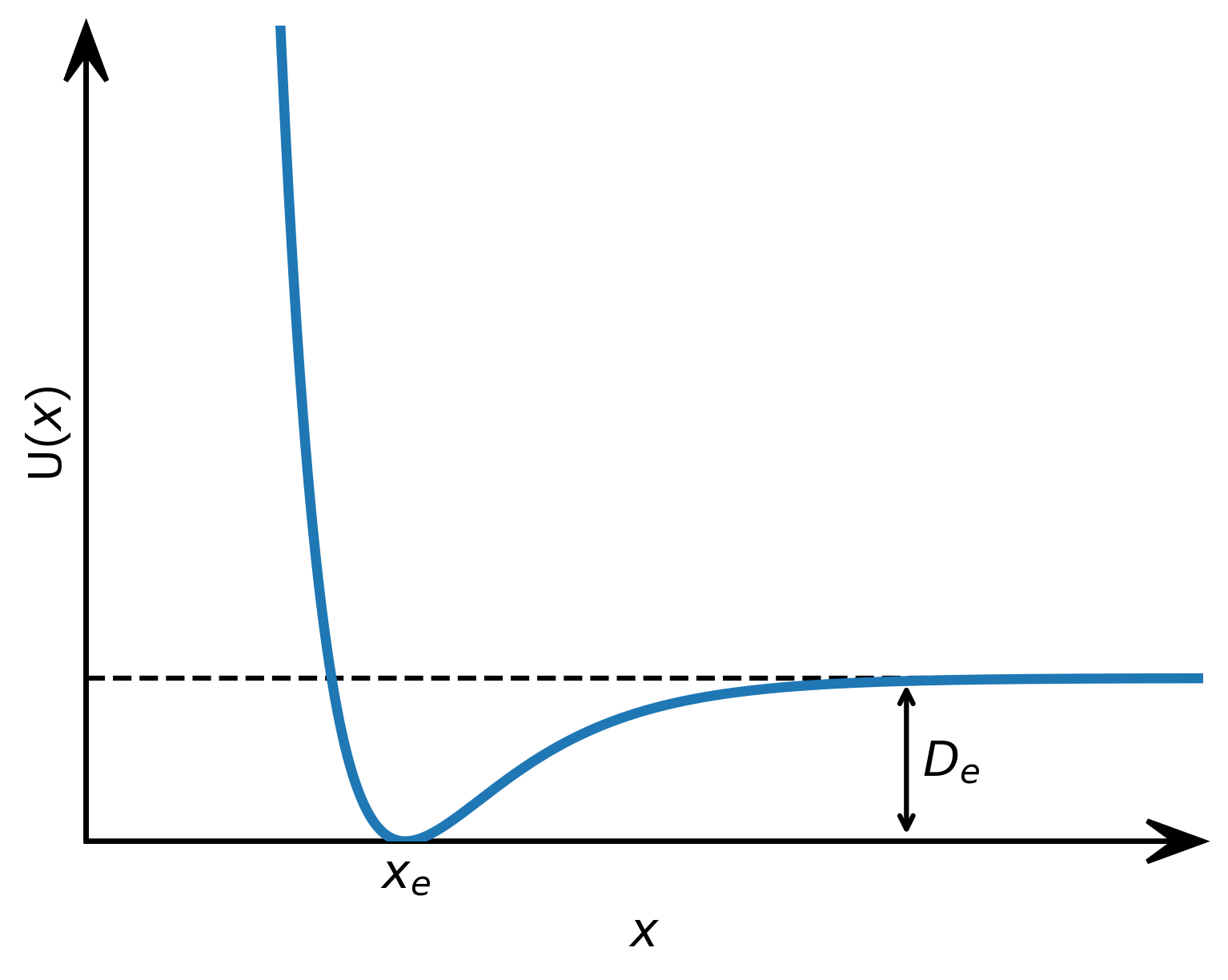
Figure 2: Graph of the Morse potential with arrowed axes and an annotation
Multi-panel figure¶
This code will read in data from an external file and draw two graphs side by side:
c = 0.52918 # bohr to angstrom conversion
def read_data(filename):
with open(filename, 'r') as f:
data = np.array(f.readlines(), dtype=np.float64)
return data[1:]
# distances
R2 = 2.3651*c
R6 = 1.4722*c
L2 = read_data('/home/markov/tmp/result_2.log') # Pt1---BCP_1_2
L6 = read_data('/home/markov/tmp/result_pt13.log') # C7---BCP_7_8
fig, ((ax1, ax2)) = plt.subplots(1, 2, figsize=(8, 4),
sharex=False, sharey=False,
gridspec_kw=({'hspace': 0.33,
'wspace': 0.33})
)
fig.patch.set_alpha(1.0) # setting transparency off
ax1.plot(np.linspace(0, R6, 100), L6, linewidth=3)
ax1.set_title(u'C-BCP (with C)', fontsize='large', **cfont)
ax2.plot(np.linspace(0, R2, 100), L2, linewidth=3)
ax2.set_title(u'Pt–BCP (with Pt)', fontsize='large', **cfont)
for item in [ax1, ax2]:
for spine in ['top', 'right']:
item.spines[spine].set_visible(False)
for spine in ['bottom', 'left']:
item.spines[spine].set_linewidth(1.5)
item.spines[spine].set_color(ccolor)
item.set_yticks([-5, 0, 5, 10])
item.tick_params(labelsize='large', length=5, width=1.5, color=ccolor)
item.set_xlim(0.25, 1.25)
item.set_ylim( -5, 15)
item.grid(axis='y', linewidth=1.5)
item.set_xlabel(u'distance from nuclear CP (Å)',
fontsize='large', **cfont)
item.set_ylabel(u'L(r) (a.u.)',
fontsize='large', **cfont)
fig.savefig('side-by-side.png', bbox_inches='tight', dpi=300, format='png')
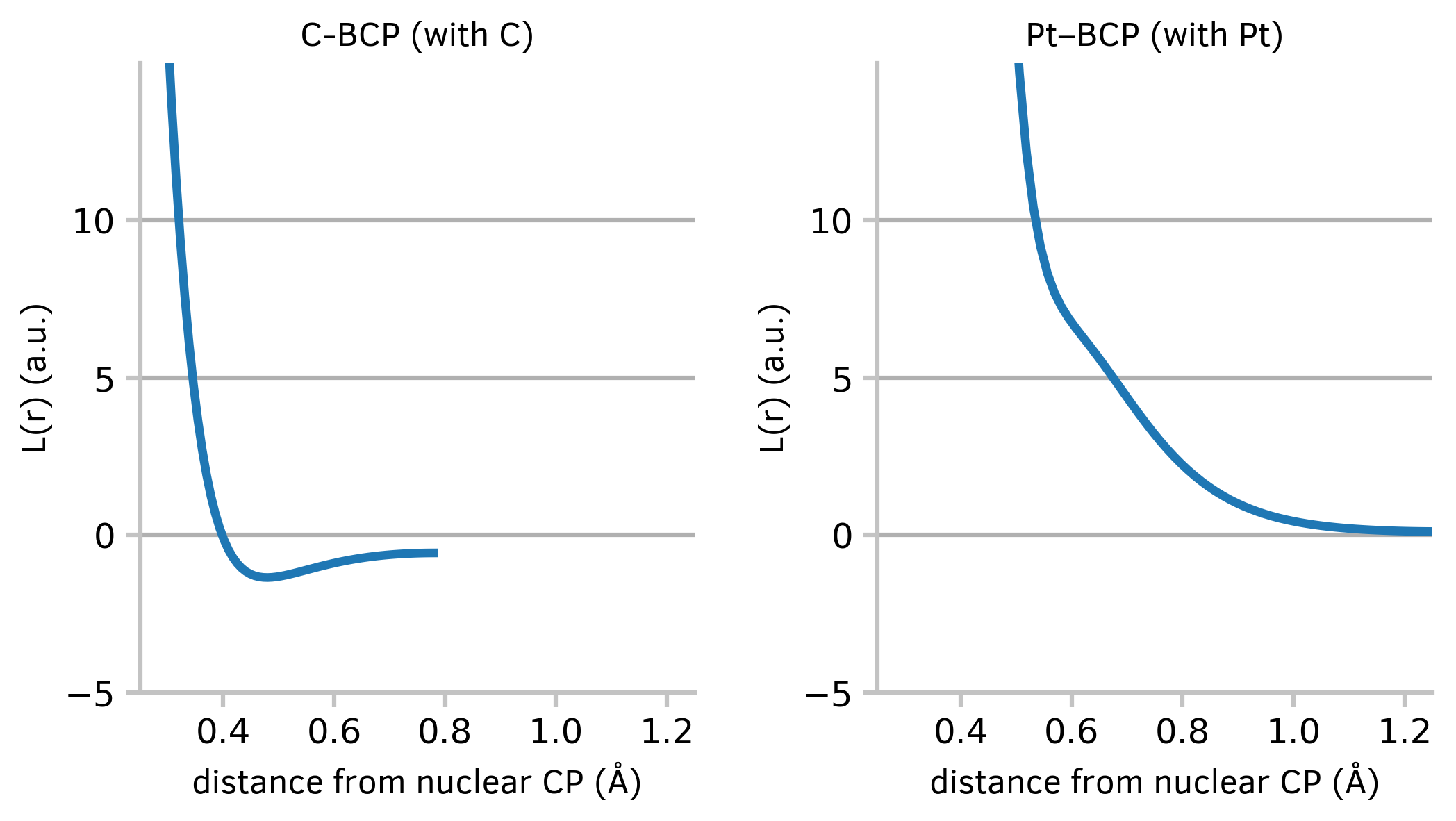
Figure 3: Two graphs of a continuous variable plotted side by side
Density plots¶
The plots of kernel density estimation of the probability density function may be useful in exploring big datasets.
First, in order to retrieve data, connect to sqlite3 databases and execute simple SQL query.
Next, construct a DataFrame which will contain both datasets. Draw graphs with convenient pandas plot method.
grid_lw = 1.33
query = 'select * from search1_DIST1;'
index_col = 'MOL_ID'
with sqlite3.connect('../tmp/pd3.8.sqlite') as conn_pd, \
sqlite3.connect('../tmp/pt3.8.sqlite') as conn_pt:
dist_pd = pd.read_sql_query(query, conn_pd, index_col=index_col)
dist_pt = pd.read_sql_query(query, conn_pt, index_col=index_col)
dist_pd = dist_pd.rename(columns={'DIST1': 'Pd-Pd distance'})
dist_pt = dist_pt.rename(columns={'DIST1': 'Pt-Pt distance'})
ax = dist_pt['Pt-Pt distance'].plot(kind='kde', figsize=(6, 4.5),
xlim=(2.3, 3.8), ylim=(0, 2),
linewidth=3,
)
dist_pd['Pd-Pd distance'].plot(kind='kde', ax=ax, linewidth=3)
ax.figure.patch.set_alpha(1.0) # setting transparency off
ax.grid(axis='both', linewidth=grid_lw)
L = ax.legend()
plt.setp(L.texts,
size='large',
**cfont) # ax.legend() can set fontsize, but not fontname
ax.spines[:].set_linewidth(grid_lw)
ax.spines[:].set_color(ccolor)
ax.tick_params(labelsize='large', length=5, width=grid_lw, color=ccolor)
ax.set_xlabel(u'R(M-M) (Å)', fontsize='x-large', **cfont)
ax.set_ylabel(u'Density', fontsize='x-large', **cfont)
ax.set_xticks([2.3, 2.6, 2.9, 3.2, 3.5, 3.8])
ax.set_yticks([0.5, 1.0, 1.5, 2.0])
ax.annotate(text=u'2.49 Å',
xy=(2.492, 0.29),
xytext=(2.31, 0.55),
arrowprops=dict(arrowstyle='simple',
facecolor='tab:blue',
edgecolor='tab:blue'),
color='tab:blue',
fontsize='large',
**cfont)
ax.annotate(u'2.70 Å', xy=(2.63, 1.9),
fontsize='large', color='tab:blue', **cfont)
ax.annotate(u'2.78 Å', xy=(2.75, 1.76),
fontsize='large', color='tab:orange', **cfont)
ax.figure.savefig('density-plots-mod.png',
bbox_inches='tight',
dpi=300, format='png')
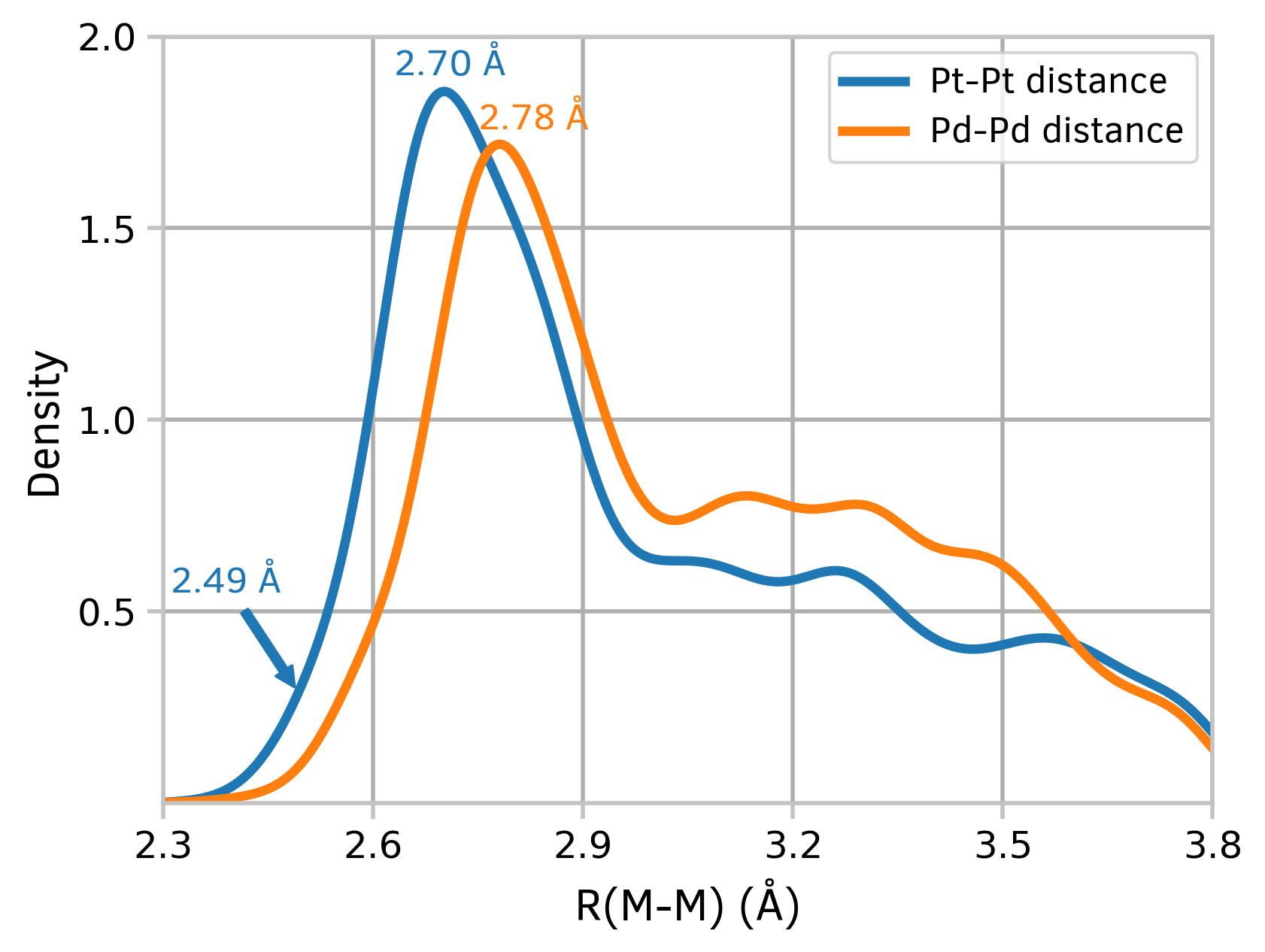
Figure 4: Kernel density estimation plots
2D hexagonal binning plots¶
A 2D hexagonal binning plot is a graphical representation of data in which a hexagonal grid is used to bin the data points. Each hexagonal bin is represented by a single point, and the value of the bin is represented by the color or size of the point. This type of plot is useful for visualizing large datasets and for identifying patterns and trends in the data. For example, fingerprint plots are the visual representation of all the intermolecular distances simultaneously, and are unique for a given crystal structure and polymorph. Here, we draw fingerprint plots for four different crystal forms of platinum acetate.
First, read in data from an external file:
def read_data(logfile, s):
with open(logfile, 'r') as f:
sw = False
a = []
for line in f:
if (r'begin ' + s) in line:
sw = True
continue
if sw:
if (r'end ' + s) in line:
sw = False
break
a.append(line)
return np.array(a, dtype=np.float64)
d_i_1 = read_data('/home/markov/tmp/cher.cxs', 'd_i')
d_e_1 = read_data('/home/markov/tmp/cher.cxs', 'd_e')
d_i_2 = read_data('/home/markov/tmp/Pt43_253.cxs', 'd_i')
d_e_2 = read_data('/home/markov/tmp/Pt43_253.cxs', 'd_e')
d_i_3 = read_data('/home/markov/tmp/1874439_platac2.cxs', 'd_i')
d_e_3 = read_data('/home/markov/tmp/1874439_platac2.cxs', 'd_e')
d_i_4 = read_data('/home/markov/tmp/1987363_pt32.cxs', 'd_i')
d_e_4 = read_data('/home/markov/tmp/1987363_pt32.cxs', 'd_e')
To draw a 2D hexagonal binning plot, you will need to use the hexbin method:
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(8, 8),
gridspec_kw=({'hspace': 0.6,
'wspace': 0.6}))
fig.patch.set_alpha(1.0) # setting transparency off
cmap = 'plasma'
fw = 'bold'
cm = ax1.hexbin(d_i_1, d_e_1, mincnt=1, cmap=cmap)
ax1.set_title(u'1', fontweight=fw, **cfont)
ax2.hexbin(d_i_2, d_e_2, mincnt=1, cmap=cmap)
ax2.set_title(u'2', fontweight=fw, **cfont)
ax3.hexbin(d_i_3, d_e_3, mincnt=1, cmap=cmap)
ax3.set_title(u'3', fontweight=fw, **cfont)
ax4.hexbin(d_i_4, d_e_4, mincnt=1, cmap=cmap)
ax4.set_title(u'4', fontweight=fw, **cfont)
cax = plt.axes([0.10, 0.48, 0.80, 0.02])
cb = fig.colorbar(cm, cax=cax, orientation='horizontal')
cax.tick_params(labelsize='medium')
for item in [ax1, ax2, ax3, ax4]:
for spine in ['top', 'right']:
item.spines[spine].set_visible(False)
for spine in ['bottom', 'left']:
item.spines[spine].set_linewidth(1.5)
item.spines[spine].set_color(ccolor)
item.set_xticks([1.0, 1.5, 2.0, 2.5])
item.tick_params(labelsize='large', length=5, width=1.5, color=ccolor)
item.set_xlim(0.5, 2.8)
item.set_ylim(0.5, 2.8)
item.set_xlabel(u'$d_i$ (Å)', **cfont)
item.set_ylabel(u'$d_e$ (Å)', **cfont)
fig.savefig('2d-binning-plots.png',
bbox_inches='tight',
dpi=300, format='png')
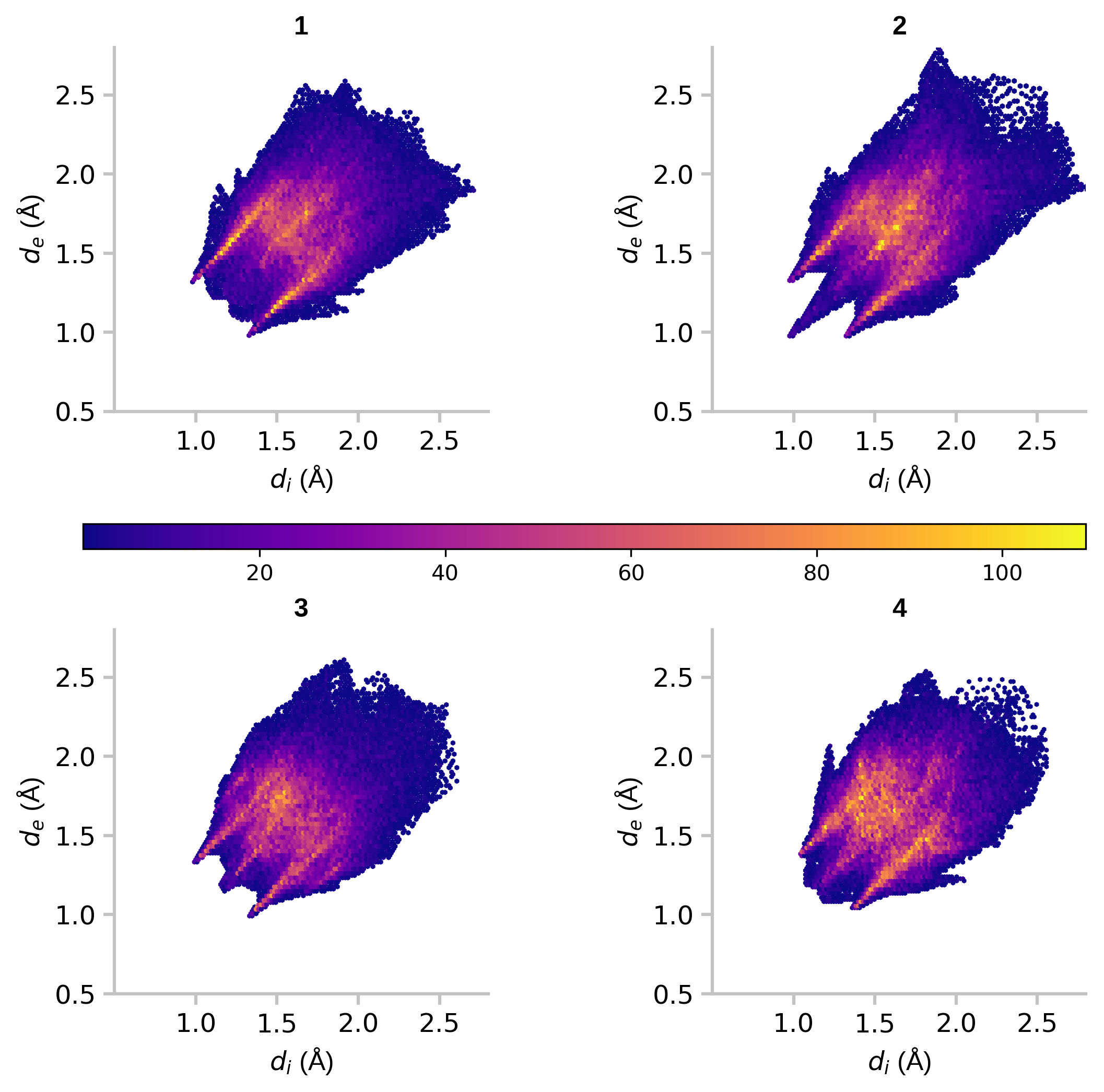
Figure 5: 2D hexagonal binning plots
References¶
Matplotlib
Jupyter Notebook
Matplotlib: Anatomy of a figure
Fundamentals of Data Visualization by Claus O. Wilke
Chartjunk by Edward Tufte from "The Visual Display of Quantitative Information"
Index of used functions and methods¶
Python¶
IPython magics¶
Matplotlib¶
- artist.setp()
- axes.annotate()
- axes.arrow()
- axes.hlines()
- axes.legend()
- axes.hexbin()
- axes.plot()
- axes.get_window_extent()
- axes.get_xlim()
- axes.get_ylim()
- axes.grid
- axes.set_title()
- axes.set_xlabel()
- axes.set_ylabel()
- axes.set_xlim()
- axes.set_ylim()
- axes.set_xticks()
- axes.set_yticks()
- axes.set_xticklabels()
- axes.set_yticklabels()
- axes.text()
- axes.tick_params()
- figure.colorbar()
- figure.dpi_scal_trans()
- figure.savefig()
- matplotlib.spines()
- patch.set_alpha()
- pyplot.subplots()